相对论量子化学计算方法

相对论量子化学是理论化学的一个重要研究分支。基于刘文剑等人提出的“精确二分量”（X2C）相对论哈密顿（也称“具有Dirac精度的NESC”），我们与国内外合作者共同开发了X2C的一系列解析导数并实现程序化，包括用于结构优化的梯度，用于振动频率、过渡态优化和化学反应模拟的Hessian，求解耦合微扰方程CPGHF/CPGKS的算法，以及偶极矩、偶极极化率、红外强度、穆斯堡尔谱（同质异能位移/接触密度、核四极分裂/EFG）、NMR等各种相对论的单电子性质。

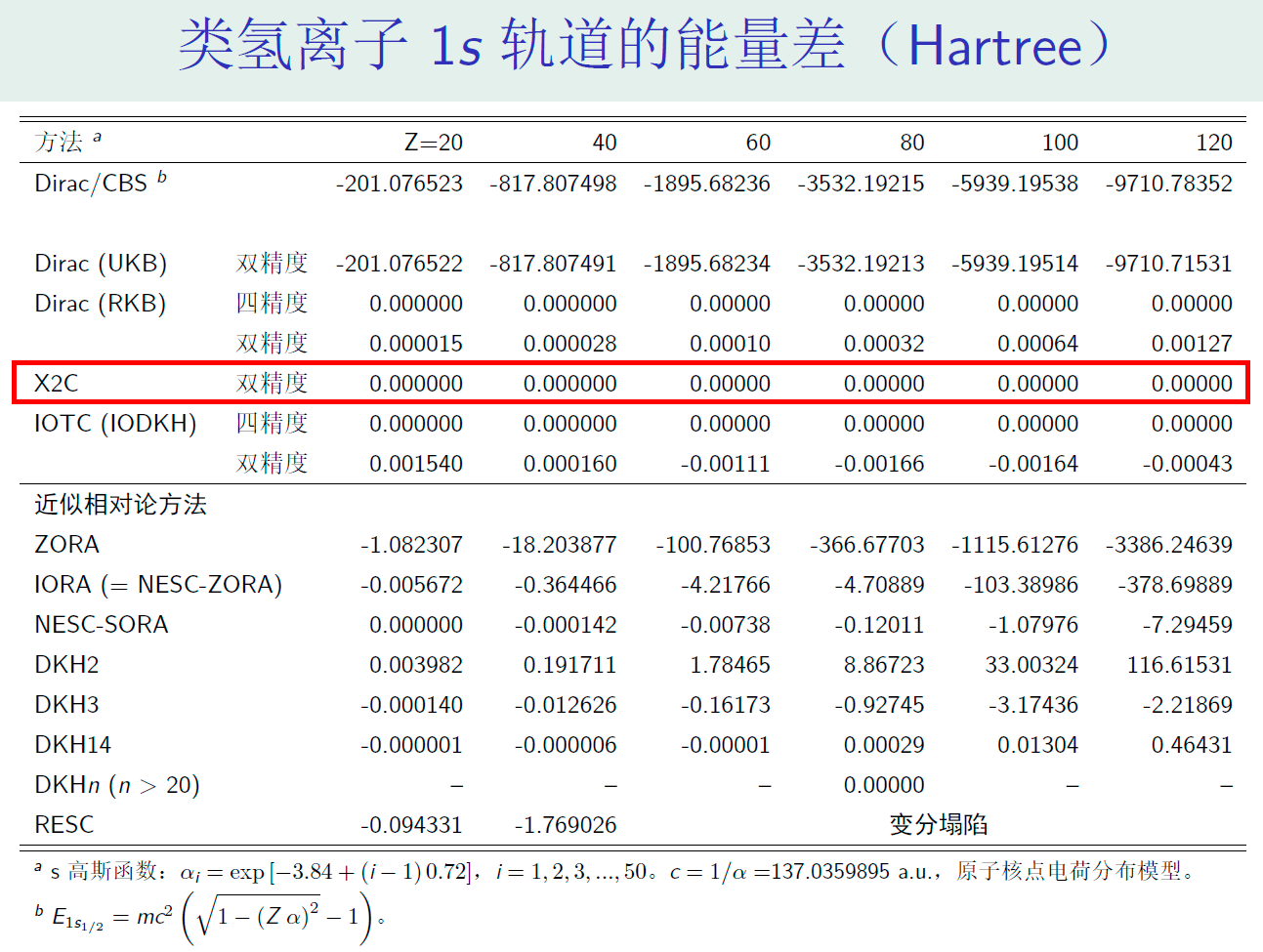
各种相对论和准相对论方法计算类氢原子1s轨道的能量或能量差（Theor. Chem. Acc. 130, 633, 2011）

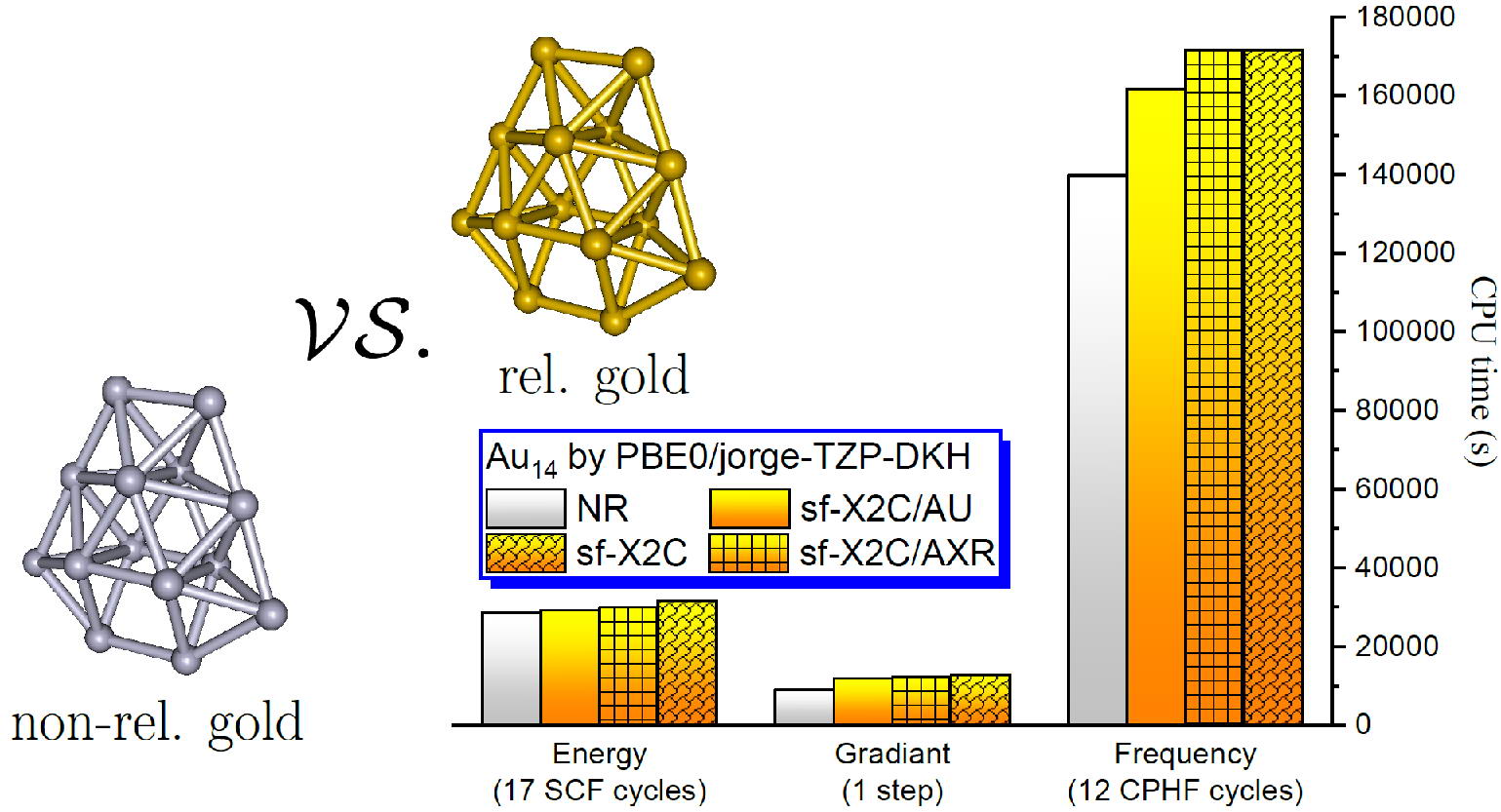
非相对论和标量相对论（sf-X2C、sf-X2C/AXR、sf-X2C/AU）DFT计算Au₁₄团簇能量、梯度、Hessian的计算时间比较^[7]

发表的部分论文如下：

[1] W. Zou, M. Filatov, and D. Cremer, Development, Implementation, and Application of an Analytic Second Derivative Formalism for the Normalized Elimination of the Small Component Method, J. Chem. Theory Comput. 8, 2617 (2012).

[2] W. Zou, M. Filatov, and D. Cremer, Analytic calculation of second-order electric response properties with the Normalized Elimination of the Small Component (NESC) method, J. Chem. Phys. 137, 084108 (2012).

[3] D. Cremer, W. Zou, and M. Filatov, Dirac-exact relativistic methods: The Normalized Elimination of the Small Component Method, WIREs Comput. Mol. Sci. 4, 436-467 (2014).

[4] W. Zou, M. Filatov, and D. Cremer, Analytical energy gradient for the two-component normalized elimination of the small component method, J. Chem. Phys. 142, 214106 (2015).

[5] T. Yoshizawa, W. Zou, and D. Cremer, Calculations of electric dipole moments and static dipole polarizabilities based on the two-component normalized elimination of the small component method, J. Chem. Phys. 145, 184104 (2016).

[6] T. Yoshizawa, M. Filatov, D. Cremer, W. Zou, Calculation of contact densities and Mössbauer isomer shifts utilising the Dirac-exact two-component normalised elimination of the small component (2c-NESC) method, Mol. Phys. 117, 1164-1171 (2019).

[7] W. Zou, G. Guo, B. Suo, and W. Liu, Analytic Energy Gradients and Hessians of Exact Two-Component Relativistic Methods: Efficient Implementation and Extensive Applications, J. Chem. Theory Comput. 16, 1541-1554 (2020).

[8] H. Zhu, C. Gao, M. Filatov, and W. Zou, Mössbauer isomer shifts and effective contact densities obtained by the exact two-component (X2C) relativistic method and its local variants, Phys. Chem. Chem. Phys. 22, 26776-26786 (2020).